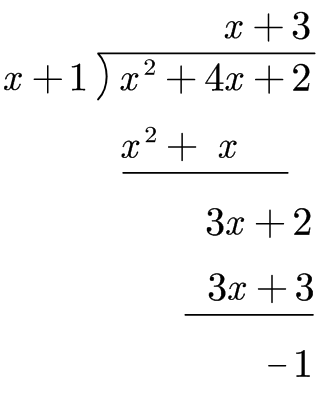从中国剩余定理到拉格朗日插值法

本文是看了b站up主乐正垂星的视频后写下的笔记（拖了足足三四个月吧），当时看的时候觉得大受震撼。可能看这篇博客不如直接看视频来的简明，但写下这篇博客仅仅是为了记录我学过这个定理。

回顾

在之前的博客中，介绍了中国剩余定理，该定理用数学表达为：

对于同余方程组

$$\begin{cases} x\equiv a_1(\mod m_1) \\ x\equiv a_2(\mod m_2) \\ \cdots\\ x\equiv a_n(\mod m_n) \end{cases}$$

其解为：

$$x\equiv\sum_{i=1}^n{a_i*M_i}*inv(M_i) (\mod M)$$

其中：

$$M=\prod_{i=1}^{n}m_i\\ M_i=\frac{M}{m_i}$$

$inv$表示乘法逆元

整式除法

在初中，我们可能会见到如下的的整式除法：

$$\frac{x^2+3x+2}{x+1}=x+2$$

这是显而易见的，因为我们可以用十字相乘法对分子式进行因式分解，但是当遇到这样的情况时，你可能会束手无策：

$$\frac{x^2+4x+2}{x+1}$$

这里引入一个新的计算方式

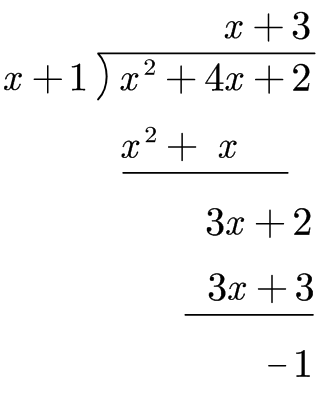
和之前学过方法有点不同，这是整式的长除法，其主要的计算思想就将一个m次多项式$f(x)$除以一个n次多项式$g(x)$,得到一个多项式的商和一个n-1次多项式$r(x)$。

多项式长除法的思想就是每次把被除数的最高项除进，这里并没有规定多项式每一项的系数都要是整数，也就是说，计算前、后多项式的系数可以是有理数甚至是无理数。

于是，我们可以尝试将数论公式推广到对于含未知数的多项式的形式，对于上面一个式子便是：

$$x^2+4x+2\equiv-1(\mod x+1)$$

写成更一般的形式：

$$f(x)\equiv r(x)(\mod m(x))$$

可以发现，之前提到的同余的加减法封闭性和乘法封闭性对于多项式的同余方程同样适用

$$a+c\equiv b+c(\mod p) \quad\Longrightarrow\quad a(x)+c(x)\equiv b(x)+c(x)(\mod m(x))\\ a*c\equiv b*c(\mod p) \quad\Longrightarrow\quad a(x)*c(x)\equiv b(x)*c(x)(\mod m(x))\\$$

但是，同余式的除法依旧十分棘手，于是又要引入逆元的概念

多项式的逆元

多项式的逆元用$f^{-1}(x)$来表示，即$f^{-1}(x)$满足

$$f(x)*f^{-1}(x)\equiv 1(\mod m(x))$$

一次多项式的特殊性质

可以证明（或者尝试说服一下自己），一次多项式的同余方程有以下几个性质（这里的$c$是常数）

$$f(x)\equiv f(a)(\mod x-a)\\ c\equiv \frac{1}{c} (\mod x-a)$$

由于$f(a)$也是常数，所以我们可以在第一个式子的左右同时乘上$\frac{1}{f(a)}$，可以得出下面这个同余方程

$$f(x)*\frac{1}{f(a)}\equiv 1(\mod x-a)$$

于是，我们得出了一次多项式的乘法逆元。

中国剩余定理的多项式形式

我们将上面得到的第一个结论写成同余方程组的形式

$$\begin{cases} f(x)\equiv f(x_1)(\mod x-x_1)\\ f(x)\equiv f(x_2)(\mod x-x_2)\\ \cdots\\ f(x)\equiv f(x_n)(\mod x-x_n) \end{cases}$$

根据中国剩余定理的内容，该同余方程的解为：

$$f(x)\equiv \sum_{i=1}^n{f(x_i)*\vec{e_i}}$$

现在要做的就是求出每个基向量$\vec{e_i}$。

我们可以根据之前的中国剩余定理，推广到多项式的形式，即

$$\vec{e_i} = M_i(x)*inv(M_i(x))$$

与之前相似

$$M_i(x)=\frac{\prod_{j=1}^n{(x-x_j)}}{x-x_i}$$

而$inv(M_i(x))$就是$M_i(x)$在模$x-x_i$意义下的乘法逆元，可以通过上面一次式的结论得出，

$$inv(M_i(x)) = \frac{1}{M_i(x_i)}$$

将这两个式子代入基向量，得到

$$\vec{e_i}=\frac{\prod_{j\neq i}(x-x_j)}{\prod_{j\neq i}(x_i-x_j)}=\prod_{j\neq i}\frac{(x-x_j)}{(x_i-x_j)}$$

所以，将这个式子代入中国剩余定理的结论

$$f(x)=\sum_{i=1}^nf(x_i)*\prod_{j\neq i}\frac{(x-x_j)}{(x_i-x_j)} (\mod M(x))$$

可以发现，这个式子恰好就是拉格朗日插值法的公式。

尝试解释

可能直接从中国剩余定理到拉格朗日插值法会有些跳跃，但是我们不妨从“实验现象”出发，尝试解释“实验现象”。

• 我们构造出的同余方程组，表达的就是在$x=x_i$时，曲线$y=f(x)$恰好经过$f(x_i)$，这可以看成是希望达到的目标，即插值后的曲线要经过已知的所有点
• 最后的结果中，出现了和中国剩余定理一样的$\mod M(x)$，这里我们可以理解为对最终结果的次数做了一个限制，即最后的$f(x)$次数为n-1，而非更大，限制了结果的个数。