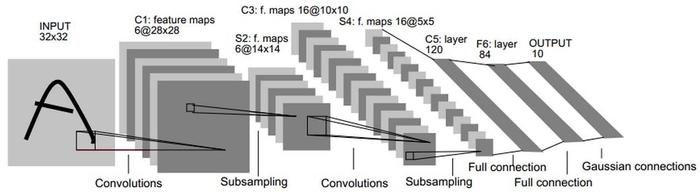
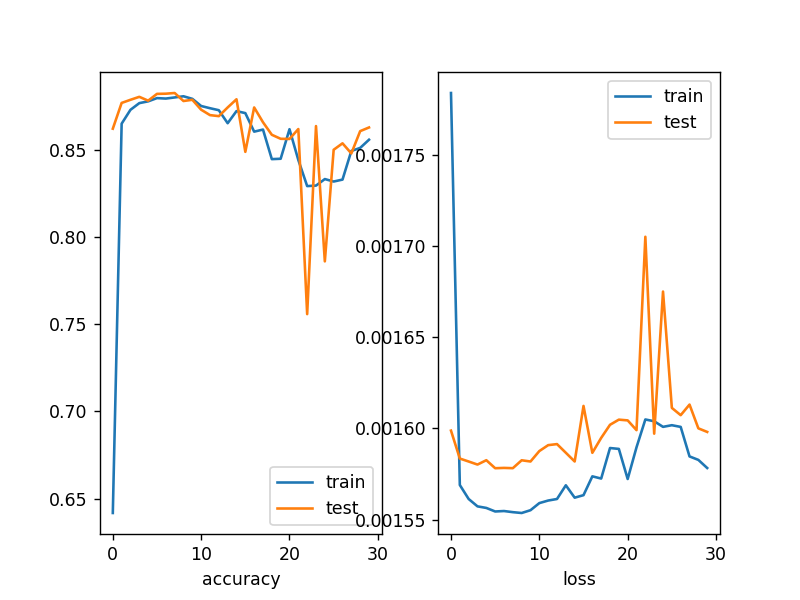
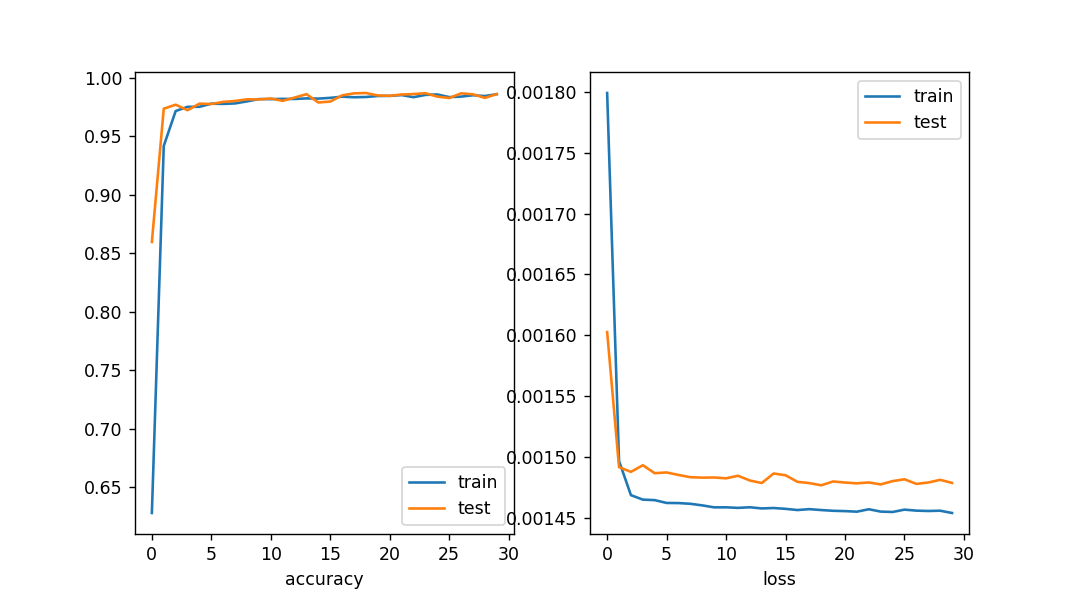
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
| import torch
import torchvision
from torch.utils.data import DataLoader
from torch import nn
from matplotlib import pyplot
down_path = ".\data"
device = torch.device("cuda")
def raw_read():
trans = torchvision.transforms.Compose([torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize(mean = [0.5],std = [0.5])])
train_raw = torchvision.datasets.MNIST(down_path,True,transform=trans,download=True)
test_raw = torchvision.datasets.MNIST(down_path,False,transform=trans,download=True)
return train_raw,test_raw
def get_loader(train_raw,test_raw,batch_size=256):
train_loader = DataLoader(dataset=train_raw,batch_size=batch_size,shuffle=True,num_workers=4,pin_memory=True)
test_loader = DataLoader(dataset=test_raw,batch_size=batch_size,num_workers=4,pin_memory=True)
return train_loader,test_loader
def train(net,optimizer,loss,train_loader):
correct = 0
tot = 0
epoch_loss = 0
net.train()
for X,y in train_loader:
X = X.to(device)
y = y.to(device)
net.zero_grad()
yhat = net(X)
y = torch.nn.functional.one_hot(y).type(torch.float32)
l = loss(yhat,y)
l.mean().backward()
optimizer.step()
cmp = yhat.argmax(dim=1)==y.argmax(dim=1)
correct += cmp.sum()
epoch_loss += l
tot += y.shape[0]
correct = correct.to(torch.device("cpu"))
epoch_loss = epoch_loss.to(torch.device("cpu")).detach()
return correct/tot,epoch_loss/tot
def test(net,loss,test_loader):
correct = 0
tot = 0
epoch_loss = 0
net.eval()
with torch.no_grad():
for X,y in test_loader:
X = X.to(device)
y = y.to(device)
yhat = net(X)
y = torch.nn.functional.one_hot(y).type(torch.float32)
l = loss(yhat,y)
cmp = yhat.argmax(dim=1)==y.argmax(dim=1)
correct += cmp.sum()
epoch_loss += l
tot += y.shape[0]
correct = correct.to(torch.device("cpu"))
epoch_loss = epoch_loss.to(torch.device("cpu")).detach()
return correct/tot,epoch_loss/tot
def start(num_epoches,net,optimizer,loss,train_loader,test_loader):
train_acc = []
train_loss = []
test_acc = []
test_loss = []
for _ in range(num_epoches):
acc,epoch_loss = train(net,optimizer,loss,train_loader)
train_acc.append(acc)
train_loss.append(epoch_loss)
acc,epoch_loss = test(net,loss,test_loader)
test_acc.append(acc)
test_loss.append(epoch_loss)
pyplot.figure()
pyplot.subplot(1,2,1)
pyplot.plot(range(num_epoches),train_acc)
pyplot.plot(range(num_epoches),test_acc)
pyplot.xlabel("accuracy")
pyplot.legend(labels=("train","test"))
pyplot.subplot(1,2,2)
pyplot.plot(range(num_epoches),train_loss)
pyplot.plot(range(num_epoches),test_loss)
pyplot.xlabel("loss")
pyplot.legend(labels=("train","test"))
pyplot.show()
if __name__ == '__main__':
batch_size = 1024
train_raw,test_raw = raw_read()
train_loader,test_loader = get_loader(train_raw,test_raw,batch_size)
net = nn.Sequential(
nn.Conv2d(kernel_size=5,padding=2,out_channels=6,in_channels=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2),
nn.ReLU(),
nn.Conv2d(kernel_size=5,in_channels=6,out_channels=16),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2),
nn.ReLU(),
nn.Conv2d(kernel_size=5,in_channels=16,out_channels=120),
nn.Flatten(),
nn.Linear(in_features=120,out_features=10),
nn.ReLU(),
nn.Softmax(dim=1)
)
net.to(device)
optimizer = torch.optim.Adam(net.parameters(),lr=0.01,weight_decay=0.001)
loss = torch.nn.CrossEntropyLoss()
start(30,net,optimizer,loss,train_loader,test_loader)
s = input("Save this model?")
if s == 'y':
torch.save(net,".\model.pth")
|