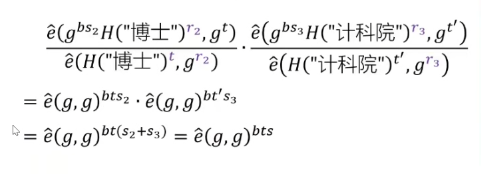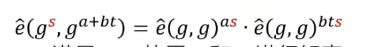CP-ABE属性基加密

前言

IMG_20230327_115132

这个实验是课程《大数据安全与隐私》的附加实验，实验难度确实挺大的，首先是实验的设计到比较深的数学原理，其次是实验环境不太好配置，需要用到很多库。个人感觉这个实验做起来还是很枯燥的，就是照着PPT调库就完事，做完了也没理解多少内容。

环境准备

首先需要一个Linux虚拟机，然后根据课件上的内容到官网下载好PBC库（以及安装前置GMP等），然后本地编译一下。我的代码还用到了OpenSSL库，这个比较棘手，因为Ubuntu自带OpenSSL3.0，但是高版本的不太好用，所以需要把自带的OpenSSL卸载，然后从官网上下载旧版本（1.0）的，再编译安装。

当然，如果不想用OpenSSL，大可以直接自行实现一个SHA1算法，只要保证正确就行。

安装完库，还需要将项目链接到库。在CLion的CMakeLists.txt中写入以下内容(ABE是你项目的名称)：

cmake_minimum_required(VERSION 3.25)
project(ABE)

find_package(OpenSSL REQUIRED)
include_directories(${OPENSSL_INCLUDE_DIR})
link_libraries(libgmp.a libgmp.so libpbc.a)

set(CMAKE_CXX_STANDARD 17)

add_executable(ABE main.cpp)

target_link_libraries(ABE libgmp.a libgmp.so libpbc.a)

target_link_libraries(ABE OpenSSL::Crypto OpenSSL::SSL)

完成后，包含头文件pbc/pbc.h和openssl/sha.h，然后随便写一下相关的函数，没有报错就可以开始写代码了。

双线性对

计算双线性对的操作比较繁琐，我们可以直接将其封装成一个函数。

void cal(element_t* res,element_t a,element_t b)
{
    element_init_GT(*res,pairing);
    pairing_pp_t temp;
    pairing_pp_init(temp,a,pairing);
    pairing_pp_apply(*res,b,temp);
}

生成公钥

公钥的形式如下，整个括号的内容其实可以看成是Python中的元组。

PK=(g,g^b,\hat{e}(g,g)^a,H)

其中H是一个哈希函数，这里我们将其定义为SHA1。 $a$ 是主密钥MSK。在初始化变量时要注意，第三个分量是经过双线性对运算之后的值，所以是群GT中的，其余两个分量都是G1中的。每个element_t类型的变量都需要被初始化，否则会出现段错误。

class Pubkey{
public:
    element_t g,g_b,egg_a,a;
    Pubkey()
    {
        element_t a,b,g,gb,egg,egga;
        // pay attention to the Group:Zr, G1 or GT
        element_init_Zr(a,pairing);
        element_init_Zr(b,pairing);
        element_init_G1(g,pairing);
        element_init_G1(gb,pairing);
        element_init_GT(egg,pairing);
        element_init_GT(egga,pairing);

        // g,a,b is random values
        element_random(g);
        element_random(a);
        element_random(b);

        element_pow_zn(gb,g,b);
        
        cal(&egg,g,g);

        element_pow_zn(egga,egg,a);

        element_init_G1(this->g,pairing);
        element_init_Zr(this->a,pairing);
        element_init_G1(this->g_b,pairing);
        element_init_GT(this->egg_a,pairing);
        element_set(this->g,g);
        element_set(this->a,a);
        element_set(this->g_b,gb);
        element_set(this->egg_a,egga);
    }
};

定义用户类

class User
{
public:
    char attr[3][10];
    element_t hash[3];
    User(const char *attr1, const char *attr2, const char *attr3)
    {
        strcpy(attr[0],attr1);
        strcpy(attr[1],attr2);
        strcpy(attr[2],attr3);

        element_init_G1(hash[0],pairing);
        element_init_G1(hash[1],pairing);
        element_init_G1(hash[2],pairing);

        element_from_str(&hash[0],attr[0]);
        element_from_str(&hash[1],attr[1]);
        element_from_str(&hash[2],attr[2]);

    }
};

用户类的存在只是为了代码可读性，并不参与运算，所以设计相对简单。当实例化一个用户对象时，其三个参数被哈希函数映射为三个element_t类型的值，用于将来的运算。其中实现了一个element_from_str函数来简化代码，该函数实现如下：

void element_from_str(element_t *e,const char str[10])
{
    unsigned char buf[20];
    SHA1((unsigned char*)str,strlen(str),buf);
    element_from_hash(*e,buf,20);
}

这个函数可以理解为上一节提到的哈希函数 $H$ ，但是SHA1计算出来是字符串类型的变量，我们还需要使用库函数element_from_hash来将其转化成可用于计算的值。

生成私钥

私钥的格式如下：

SK = (g^{a+bt},g^t,H(^"attr1^"),H(^"attr2^"),\cdots)

其中t是每个私钥特异的元素，但是t不能直接表示在元组中，所以利用了离散对数难解性来隐藏t。每个私钥特异的t，也是保证两个人的私钥不能实现共谋攻击的主要手段。

私钥类的构造函数需要传入公钥类Pubkey（使用其中的a、b）和用户类User（使用其中的哈希值）作为参数，具体实现步骤如下：

class SecretKey
{
public:
    element_t g_abt,gt,h_t[3];
    SecretKey(Pubkey pk, User user)
    {
        init_all();
        element_t t;
        element_init_Zr(t,pairing);
        element_random(t);

        element_t temp1;
        element_init_G1(temp1,pairing);
        element_pow_zn(temp1,pk.g,pk.a);
        element_pow_zn(g_abt,pk.g_b,t);
        element_mul(g_abt,g_abt,temp1);

        element_pow_zn(gt,pk.g,t);

        element_pow_zn(h_t[0],user.hash[0],t);
        element_pow_zn(h_t[1],user.hash[1],t);
        element_pow_zn(h_t[2],user.hash[2],t);
    }

    void init_all()
    {
        element_init_G1(g_abt,pairing);
        element_init_G1(gt,pairing);
        element_init_G1(h_t[0],pairing);
        element_init_G1(h_t[1],pairing);
        element_init_G1(h_t[2],pairing);
    }
};

密文生成

密文的格式如下：

\large CT = (M*\hat{e}(g,g)^{as},g^s,C_1,C_2,\cdots)\\ \large where \space C_i=(g^{bs_i}*H(^"attr_i^")^{r_i},g^{r_i})

可以看到，密文中不仅包含需要加密的数据（利用双线性对加密），还包含一个 $g^s$ 用来隐藏访问控制的值 $s$ ，以及若干个用于访问控制的Ci，我们姑且称它为子密文。子密文各包含一个访问控制的值r（同样用离散对数难解性）来隐藏，以及一个分量，这个分量用于后续解密的计算，如果符合密文约定的访问控制规则，就会恰好与私钥的分量抵消，这点之后会看到。

M是明文，如果只是想实现实验的阶梯一和阶梯二，那么简单地把M看成的 $Z_r$ 群的一个随机元素即可。

为了代码更整洁，这里单独把子密文实现为一个类：

那个空的构造函数是默认构造函数，不加上的话之后的密文类会报错，由于不是很了解C++只能用这种笨办法写。

class SubCipher{
public:
    element_t g_bs_H,g_r;
    SubCipher()
    {
		
    }
    SubCipher(Pubkey pk, const char attr[10], element_t s)
    {
        init_all();
        element_t r;
        element_init_Zr(r,pairing);
        element_random(r);

        element_pow_zn(g_r,pk.g,r);

        element_t H_r,H;
        element_init_G1(H_r,pairing);
        element_init_G1(H,pairing);
        element_from_str(&H,attr);

        element_pow_zn(H_r,H,r);
        element_pow_zn(g_bs_H,pk.g_b,s);
        element_mul(g_bs_H,g_bs_H,H_r);
    }

    void init_all()
    {
        element_init_G1(g_bs_H,pairing);
        element_init_G1(g_r,pairing);
    }
};

密文类：

class Cipher{
public:
    element_t M_egg_as,g_s;
    SubCipher C[3];
    Cipher(Pubkey pk, element_t M) {
        element_t s[3],ss,r;
        element_init_Zr(ss,pairing);
        element_init_Zr(r,pairing);
        element_init_Zr(s[0],pairing);
        element_init_Zr(s[1],pairing);
        element_init_Zr(s[2],pairing);
        element_init_GT(M_egg_as,pairing);
        element_init_G1(g_s,pairing);

        element_random(ss);
        element_random(r);
		
        // Access control policy, refering to lecture slices
        element_set(s[0],ss);
        element_set(s[1],r);
        element_sub(s[2],ss,r);

        C[0] = SubCipher(pk,"Prof",s[0]);
        C[1] = SubCipher(pk,"CS",s[1]);
        C[2] = SubCipher(pk,"Teacher",s[2]);

        element_pow_zn(g_s,pk.g,ss);

        element_pow_zn(M_egg_as,pk.egg_a,ss);
        element_mul(M_egg_as,M_egg_as,M);
    }
};

密文类中包含三个子密文成员，分别用于三个属性的控制。需要注意的是，访问三个属性的r是需要根据属性之间的逻辑关系来设置的，“或”逻辑关系直接赋值即可，“且”逻辑关系要使用减法来完成，具体可以参考课件，结合树状图来理解更好。

本代码中的访问控制语义为：”教授“或者（”计科院“且”老师“）可以访问。

解密

属性基加密的方法是比较奇怪的，因为即使属性不符合访问控制的要求，也可以从密文中解密出一段数据，只是解密出的不是明文而大概率是乱码。而又因为属性基加密的逻辑中具有“或”逻辑，所以需要多次解密，再判断哪个才是真正的明文。依照本实验的访问控制语义，需要进行两次解密。

解密的公式如下：

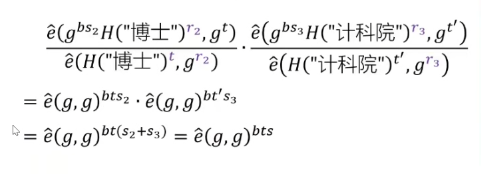
第一步求出 $\hat{e}(g,g)^{bts}$ ，又由双线性对的性质：

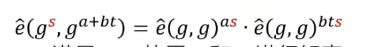
所以将 $\hat{e}(g^s,g^{a+bt})$ 除以第一步得到的值就可以获得 $\hat{e}(g,g)^{as}$ 。

最后用密文第一个分量除以这个值，就可以获得M。

上面说“博士”、“计科院”是“且”的关系，所以需要相乘。比如“教授”属性不需要与其他相“且”，则只求一个分式的值就可以。

代码如下：

void Decrypt(Cipher cipher,SecretKey secretKey,element_t *res1,element_t *res2)
{

    element_t egg_bts,fm,fz;
    element_init_GT(egg_bts,pairing);
    element_init_GT(fz,pairing);
    element_init_GT(fm,pairing);
	
    // "Prof"
    cal(&fz,cipher.C[0].g_bs_H,secretKey.gt);
    cal(&fm,secretKey.h_t[0],cipher.C[0].g_r);
	
    element_div(egg_bts,fz,fm);

    element_t e_gs_gabt;
    element_init_GT(e_gs_gabt,pairing);
    cal(&e_gs_gabt,cipher.g_s,secretKey.g_abt);

    element_t egg_as;
    element_init_GT(egg_as,pairing);
    element_div(egg_as,e_gs_gabt,egg_bts);

    element_div(*res1,cipher.M_egg_as,egg_as);
	
    // "CS" and "Teacher"
    element_t fs1,fs2,fz1,fz2,fm1,fm2;
    element_init_GT(fs1,pairing);
    element_init_GT(fs2,pairing);
    element_init_GT(fz1,pairing);
    element_init_GT(fz2,pairing);
    element_init_GT(fm1,pairing);
    element_init_GT(fm2,pairing);

    cal(&fz1,cipher.C[1].g_bs_H,secretKey.gt);
    cal(&fm1,secretKey.h_t[1],cipher.C[1].g_r);
    cal(&fz2,cipher.C[2].g_bs_H,secretKey.gt);
    cal(&fm2,secretKey.h_t[2],cipher.C[2].g_r);
    element_div(fs1,fz1,fm1);
    element_div(fs2,fz2,fm2);
    element_mul(egg_bts,fs1,fs2);
    element_div(egg_as,e_gs_gabt,egg_bts);
    element_div(*res2,cipher.M_egg_as,egg_as);

}

计算后会得到两个值，存在res1和res2中，还需要判断是否正确解密。

下面是验证共谋攻击的一个函数，其实和解密大同小异，就是把两个私钥的分量交叉使用，看是否可以正确解密：

void together(Cipher cipher,SecretKey secretKey1,SecretKey secretKey2,element_t *res)
{
    element_t egg_bts;
    element_init_GT(egg_bts,pairing);
    element_t e_gs_gabt;
    element_init_GT(e_gs_gabt,pairing);
    cal(&e_gs_gabt,cipher.g_s,secretKey1.g_abt);

    element_t egg_as;
    element_init_GT(egg_as,pairing);
    element_div(egg_as,e_gs_gabt,egg_bts);

    element_t fs1,fs2,fz1,fz2,fm1,fm2;
    element_init_GT(fs1,pairing);
    element_init_GT(fs2,pairing);
    element_init_GT(fz1,pairing);
    element_init_GT(fz2,pairing);
    element_init_GT(fm1,pairing);
    element_init_GT(fm2,pairing);

    cal(&fz1,cipher.C[1].g_bs_H,secretKey1.gt);
    cal(&fm1,secretKey1.h_t[1],cipher.C[1].g_r);
    cal(&fz2,cipher.C[2].g_bs_H,secretKey2.gt);
    cal(&fm2,secretKey2.h_t[2],cipher.C[2].g_r);
    element_div(fs1,fz1,fm1);
    element_div(fs2,fz2,fm2);
    element_mul(egg_bts,fs1,fs2);
    element_div(egg_as,e_gs_gabt,egg_bts);
    element_div(*res,cipher.M_egg_as,egg_as);
}

验证

将Alice的属性设置为(Master, CS, Assistant)，Bob设置为(Prof, EE, Teacher)，结果是Alice解密错误，而Bob的res1解密成功，res2解密失败。如果在共谋攻击中把Bob的Teacher分量借给Alice使用，则还是无法解密，验证了ABE可以抵抗共谋攻击的特点。

如果将Alice设置为(Master, CS, Teacher)而Bob不变，则可以发现两者都解密成功。但是有趣的是，Alice和Bob共谋攻击后反而不成功，这就是ABE的奇妙之处，由于各个密钥的t值不同，所以无论怎样，混合使用始终无法解开密文。

代码下载

课内

#大数据安全

CP-ABE属性基加密

http://zhouhf.top/2023/04/14/CP-ABE属性基加密/

作者

周洪锋

发布于

2023年4月14日

许可协议

C#学习笔记（二）——类、委托、接口上一篇

Socket编程（五）——多线程下一篇