为了更好地研究密码学,本着“磨刀不误砍柴工”的想法,对本科时学习的《离散数学》进行一个复习。不一样的是,这次直接对抽象代数(特别是其中的群论、环论、域论)进行再次探索。参考书目为Joseph J. Rotman 的《Advanced Modern Algebra》以及丘维声 的《抽象代数基础》。对于我认为重要的定理,我会记录下来并附加上主观感受,并不会给上详细证明。
这篇博客先主要复习群论,其余之后再说。
定义 :设n ≥ 1 n\ge1 n ≥ 1 ζ n = 1 \zeta^n=1 ζ n = 1 ζ \zeta ζ n n n
定理 :每个n n n
e 2 π i k / n = cos ( 2 π k n ) + i sin ( 2 π k n ) e^{2\pi ik/n}=\cos(\frac{2\pi k}{n})+i\sin(\frac{2\pi k}{n})
e 2 π i k / n = cos ( n 2 π k ) + i sin ( n 2 π k )
如果将这些复数根画到平面直角坐标系中,会发现这些根正好将单位元分成了n n n
定义 :如果ζ \zeta ζ n n n d d d ζ d = 1 \zeta^d=1 ζ d = 1 ζ \zeta ζ d d d
定理 :如果n n n ζ \zeta ζ d d d d ∣ n d|n d ∣ n
定义 :d d d
Φ d ( x ) = ∏ 1 ≤ i ≤ d ( x − ζ i ) \Phi_d(x) = \prod_{1\le i\le d}(x-\zeta_i)
Φ d ( x ) = 1 ≤ i ≤ d ∏ ( x − ζ i )
这里ζ i \zeta_i ζ i i i i
定理 :对于每个整数n ≥ 1 n\ge1 n ≥ 1
x n − 1 = ∏ d ∣ n Φ d ( x ) x^n-1 = \prod_{d|n}\Phi_d(x)
x n − 1 = d ∣ n ∏ Φ d ( x )
其中d d d n n n Φ 1 ( x ) , Φ n ( x ) \Phi_1(x),\Phi_n(x) Φ 1 ( x ) , Φ n ( x )
定义 :欧拉ϕ \phi ϕ 为n n n
ϕ ( n ) = deg ( Φ n ( x ) ) \phi(n) = \deg(\Phi_n(x))
ϕ ( n ) = deg ( Φ n ( x ) )
定义 :群 是指配置了二元运算∗ * ∗ G G G
结合律成立,即对任何x , y , z ∈ G x,y,z\in G x , y , z ∈ G x ∗ ( y ∗ z ) = ( x ∗ y ) ∗ z x*(y*z)=(x*y)*z x ∗ ( y ∗ z ) = ( x ∗ y ) ∗ z
存在幺元 。
每个元素都存在逆元。
如果一个群G G G G G G 阿贝尔群 。
定理 :群有如下性质:
消去律成立,如果x ∗ a = x ∗ b x*a=x*b x ∗ a = x ∗ b a ∗ x = b ∗ x a*x=b*x a ∗ x = b ∗ x a = b a=b a = b
幺元唯一。
每个元素的逆元唯一。
一个元素逆元的逆元,就是它自己。
∀ a , b ∈ G , ( a b ) − 1 = b − 1 a − 1 \forall a,b\in G, \ (ab)^-1=b^{-1}a^{-1} ∀ a , b ∈ G , ( a b ) − 1 = b − 1 a − 1
定义 :a a a G G G k ≥ 1 k\ge1 k ≥ 1 a k = e a^k=e a k = e a a a 阶 ,如果没有这样的幂存在,称a a a
定理 :如果a ∈ G a\in G a ∈ G n n n a m = 1 a^m=1 a m = 1 n ∣ m n|m n ∣ m
定理 :如果一个群是有限的,那么所有元素的阶都有限。
定义 :称群G G G H H H
运算在H H H
e ∈ H e \in H e ∈ H 如果x ∈ H x\in H x ∈ H x − 1 ∈ H x^{-1}\in H x − 1 ∈ H
不难证明,实际上只要满足上述条件的(1)和(3)即可,而对于有限群,只需要满足封闭性即是子群 。
子群给我们的启示是,如果一个在集合上的运算很难证明结合律,那么可以考虑证明这个集合是某个群的子群。
一个更简洁的证明子群的的方法:
定理 :群G G G H H H H H H x , y ∈ H x,y\in H x , y ∈ H x y − 1 ∈ H xy^{-1}\in H x y − 1 ∈ H
定理 :若干个子群的交集也是G G G
定义 :如果G G G a ∈ G a\in G a ∈ G
< a > = { a n ∣ n ∈ Z } \left<a\right>=\{a^n|n\in \Z\}
⟨ a ⟩ = { a n ∣ n ∈ Z }
为G G G a a a 循环子群 。如果存在a ∈ G a\in G a ∈ G < a > = G \left< a\right>=G ⟨ a ⟩ = G G G G a a a G G G
特别地,< ∅ > = 1 \left<\varnothing\right>={1} ⟨ ∅ ⟩ = 1
定理 :如果G = < a > G=\left<a\right> G = ⟨ a ⟩ n n n a k a^k a k G G G g c d ( k , n ) = 1 gcd(k,n)=1 g c d ( k , n ) = 1 G G G ϕ ( n ) \phi(n) ϕ ( n )
定理 :如果G G G a ∈ G a\in G a ∈ G ∣ < a > ∣ |\left<a\right>| ∣ ⟨ a ⟩ ∣
定理 :素数阶的群均为循环群。
定理 :如果X X X G G G X X X < X > \left<X\right> ⟨ X ⟩ X X X X X X
定义 :如果H H H G G G a ∈ G a\in G a ∈ G G G G a H aH a H 陪集 ,这里
a H = { a h ∣ h ∈ H } aH = \{ah|h\in H\}
a H = { a h ∣ h ∈ H }
上述所记的是左陪集,如果使用右乘,则为右陪集,左陪集和右陪集一般是不同的。另外,在一般情况下陪集不是子群。
定理 :如果H H H G G G a , b ∈ G a,b\in G a , b ∈ G
a H = b H aH=bH a H = b H b − 1 a ∈ H b^{-1}a\in H b − 1 a ∈ H a H = H aH=H a H = H a ∈ H a\in H a ∈ H 如果a H ∩ b H ≠ ∅ aH\cap bH\neq\varnothing a H ∩ b H = ∅ a H = b H aH=bH a H = b H
对一切a ∈ G a\in G a ∈ G ∣ a H ∣ = ∣ H ∣ |aH|=|H| ∣ a H ∣ = ∣ H ∣
作为(1)的对偶,H a = H b Ha=Hb H a = H b a b − 1 ∈ H ab^{-1}\in H a b − 1 ∈ H
这个定理告诉我们,陪集要么相等,要么没有交集,更进一步说,陪集就是G G G R : a R b ⇔ b − 1 a ∈ H R:aRb\Leftrightarrow b^{-1}a\in H R : a R b ⇔ b − 1 a ∈ H
定理(拉格朗日定理) :如果H H H G G G ∣ H ∣ |H| ∣ H ∣ ∣ G ∣ |G| ∣ G ∣
反之不一定成立,并不是对于所有∣ G ∣ |G| ∣ G ∣
定理 :如果 G G G a ∈ G a\in G a ∈ G ∣ G ∣ |G| ∣ G ∣
因为a a a ∣ < a > ∣ |\left< a\right>| ∣ ⟨ a ⟩ ∣ G G G a ∈ G a\in G a ∈ G ∣ < a > ∣ |\left<a\right>| ∣ ⟨ a ⟩ ∣
定理 :如果 G G G a ∈ G a\in G a ∈ G a ∣ G ∣ = 1 a^{|G|}=1 a ∣ G ∣ = 1
利用这个定理可以证明费马小定理。
定义 :G G G H H H 指数 是指G G G H H H [ G : H ] [G:H] [ G : H ]
[ G : H ] = ∣ G ∣ / ∣ H ∣ [G:H]=|G|/|H|
[ G : H ] = ∣ G ∣ / ∣ H ∣
定义 :对于模 m m m I m I_m I m U ( I m ) U(I_m) U ( I m )
U ( I m ) = { [ r ] ∈ I m ∣ gcd ( r , m ) = 1 } U(I_m) = \{[r]\in I_m|\gcd(r,m)=1\}
U ( I m ) = { [ r ] ∈ I m ∣ g cd( r , m ) = 1 }
它是阶为ϕ ( m ) \phi(m) ϕ ( m ) p p p U ( I p ) = I p × U(I_p)=I_p^\times U ( I p ) = I p × p − 1 p-1 p − 1 I p × I_p^{\times} I p × I p I_p I p
定理(费马小定理) :
a p ≡ a m o d p a p − 1 ≡ 1 m o d p a^p\equiv a\mod p\\
a^{p-1}\equiv 1 \mod p
a p ≡ a m o d p a p − 1 ≡ 1 m o d p
把I m × I_m^{\times} I m ×
定理(欧拉定理) :如果gcd ( r , m ) = 1 \gcd(r,m)=1 g cd( r , m ) = 1
r ϕ ( m ) ≡ 1 m o d m r^{\phi(m)}\equiv 1 \mod m
r ϕ ( m ) ≡ 1 m o d m
欧拉定理是对费马小定理的推广,实质上,是在U ( I m ) U(I_m) U ( I m )
定义 :如果( G , ∗ ) , ( H , ∘ ) (G,*),(H,\circ) ( G , ∗ ) , ( H , ∘ ) f : G → H f:G\rarr H f : G → H
f ( x ∗ y ) = f ( x ) ∘ f ( y ) f(x*y) = f(x)\circ f(y)
f ( x ∗ y ) = f ( x ) ∘ f ( y )
如果这个函数是双射,则称为同构 ,记为G ≅ H G\cong H G ≅ H f f f f f f G , H G,H G , H
定理 :群同态下,幺元、逆元、阶都可以保持。
定义 :f : G → H f:G\rarr H f : G → H
ker f = { x ∈ G ∣ f ( x ) = 1 } im f = { h ∈ H ∣ ∃ x ∈ G → h = f ( x ) } \ker f = \{x\in G|f(x)=1\}\\
\textrm{im} \ f=\{h\in H|\exist x\in G\rarr h=f(x)\}
ker f = { x ∈ G ∣ f ( x ) = 1 } im f = { h ∈ H ∣ ∃ x ∈ G → h = f ( x ) }
ker f \ker f ker f f f f im f \textrm{im}\ f im f f f f
定理 :设f : G → H f:G\rarr H f : G → H
ker f \ker f ker f G G G i m f im \ f i m f H H H 如果x ∈ ker f , a ∈ G x\in \ker f,a\in G x ∈ ker f , a ∈ G a x a − 1 ∈ ker f axa^{-1}\in \ker f a x a − 1 ∈ ker f
f f f ker f = 1 \ker f={1} ker f = 1
定义 :如果∀ k ∈ K , g ∈ G → g k g − 1 ∈ K \forall k\in K,g\in G\rarr gkg^{-1}\in K ∀ k ∈ K , g ∈ G → g k g − 1 ∈ K G G G K K K 正规子群 ,记为K ◃ G K\triangleleft G K ◃ G
显然,同态的核恒为正规子群。
又不难发现,阿贝尔群的每个子群都是正规子群,因为∀ k ∈ K , g ∈ G , g k g − 1 = k g g − 1 = k ∈ K \forall k\in K,g\in G, gkg^{-1}=kgg^{-1}=k\in K ∀ k ∈ K , g ∈ G , g k g − 1 = k g g − 1 = k ∈ K
定义 :如果G G G a ∈ G a\in G a ∈ G
g a g − 1 gag^{-1}
g a g − 1
的G G G a a a 共轭元素 。
在线性代数中,两个相似的矩阵互为共轭元素,即B = P A P − 1 B = PAP^{-1} B = P A P − 1
定义 :如果G G G g ∈ G g\in G g ∈ G γ g : G → G \gamma_g: G\rarr G γ g : G → G a ∈ G a\in G a ∈ G
γ g ( a ) = g a g − 1 \gamma_g (a)= gag^{-1}
γ g ( a ) = g a g − 1
定理 :共轭γ a ( g ) \gamma_a(g) γ a ( g )
这个比较显而易见,如果你已经理解“群的每次运算实际上都是一次置换(从运算表理解)”
定理 :共轭元素有相同的阶。
定理 :如果H H H G G G g ∈ G , g 2 ∈ H g\in G,g^2\in H g ∈ G , g 2 ∈ H
定理 :如果H H H G G G H H H G G G
定义 :GL(2,\C) 中下列元素
Q = { I , A , A 2 , A 3 , B , B A , B A 2 , B A 3 } A = [ 0 1 − 1 0 ] , B = [ 0 i − i 0 ] Q = \{I,A,A^2,A^3,B,BA,BA^2,BA^3\}\\
A = \begin{bmatrix}
0 & 1\\
-1 & 0
\end{bmatrix},
B=\begin{bmatrix}
0 & i\\
-i & 0
\end{bmatrix}
Q = { I , A , A 2 , A 3 , B , B A , B A 2 , B A 3 } A = [ 0 − 1 1 0 ] , B = [ 0 − i i 0 ]
组成的8阶群Q Q Q 四元数群 ,其中I I I
定义 :每个子群都是正规子群的非阿贝尔有限群叫做哈密顿群 。
定理 :每个哈密顿群形为Q × A Q\times A Q × A A A A
定义 :群G的非空子集的集合上的一种运算:
X Y = { x y ∣ x ∈ X , y ∈ Y } XY = \{xy|x\in X, y\in Y\}
X Y = { x y ∣ x ∈ X , y ∈ Y }
定理 :群G G G K K K g ∈ G g\in G g ∈ G
g K = K g gK=Kg
g K = K g
由此,正规子群的左陪集也是右陪集。
说服一下自己,元素和子群的乘积也可以用消去律,这个定理即可得证。
定理 :
通过H H H K K K G G G H K HK H K G G G H K = K H HK=KH H K = K H
如果H H H K K K G G G H K HK H K
同上面一样,把子群之间的乘积也看成一种群运算,满足消去律,则这个定理可以被接受。
定义 :商群G / K G/K G / K
G / K = { g K ∣ g ∈ G } G/K = \{gK|g\in G\}
G / K = { g K ∣ g ∈ G }
也即所有左陪集所组成的集合。
其阶∣ G / K ∣ = [ G : K ] = ∣ G ∣ / ∣ K ∣ |G/K|=[G:K]=|G|/|K| ∣ G / K ∣ = [ G : K ] = ∣ G ∣ / ∣ K ∣
定理 :如果K K K a , b ∈ G a,b\in G a , b ∈ G
a K b K = a b K aKbK = abK
a K b K = a b K
且G / K G/K G / K
此定理可以用子群之间乘法“结合律”以及“左右陪集相等”来证明。
直观地看,正规子群的运算有传递性。另外,陪集之间的运算并不依赖代表元。
定理 :每个正规子群K ◃ G K\triangleleft G K ◃ G
定义 :自然映射 π : G → G / K \pi:G\rarr G/K π : G → G / K π ( a ) = a K \pi(a)=aK π ( a ) = a K
用此公式可以把上上条定理写为:π ( a ) π ( b ) = π ( a b ) \pi(a)\pi(b)=\pi(ab) π ( a ) π ( b ) = π ( a b ) π \pi π
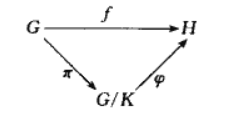
定理(第一同构定理) :如果f : G → H f:G\rarr H f : G → H
ker f ◃ G G / ker f ≅ im f \ker f\triangleleft G\\
G/\ker f \cong \textrm{im}\ f
ker f ◃ G G / ker f ≅ im f
这个定理讲了两件事,一是每个同态的核都是一个正规子群(这个在之前就提到过);二是G G G f f f G / ker f G/\ker f G / ker f im f \textrm{im} f im f ϕ : a K ↦ f ( a ) \phi:aK\mapsto f(a) ϕ : a K ↦ f ( a ) π : G → G / K \pi:G\rarr G/K π : G → G / K π : a ↦ a K \pi:a\mapsto aK π : a ↦ a K
商群R / Z R/Z R / Z R / Z ≅ S 1 R/Z\cong S^1 R / Z ≅ S 1 S 1 S^1 S 1
定理(乘积公式) :如果H , K H,K H , K G G G
∣ H K ∣ ∣ H ∩ K ∣ = ∣ H ∣ ∣ K ∣ |HK||H\cap K| = |H||K|
∣ H K ∣ ∣ H ∩ K ∣ = ∣ H ∣ ∣ K ∣
定理(第二同构定理) :如果H , K H,K H , K G G G H ◃ G H\triangleleft G H ◃ G H K HK H K H ∩ K ◃ K H\cap K\triangleleft K H ∩ K ◃ K
K / ( H ∩ K ) ≅ H K / H K/(H\cap K)\cong HK/H
K / ( H ∩ K ) ≅ H K / H
定理(第三同构定理) :如果H , K H,K H , K G G G K ≤ H K\le H K ≤ H H / K ◃ G / K H/K\triangleleft G/K H / K ◃ G / K
( G / K ) ( H / K ) ≅ G / H (G/K)(H/K) \cong G/H
( G / K ) ( H / K ) ≅ G / H
定理 :如果G G G d d d ∣ G ∣ |G| ∣ G ∣ G G G d d d
之前提到过对于一般的群来说,"d d d ∣ G ∣ |G| ∣ G ∣ G G G d d d
定义 :定义群之间的直积运算为
H × K = { ( h h ′ , k k ′ ) ∣ h , h ′ ∈ H , k , k ′ ∈ K } H\times K =\{(hh\prime,kk\prime)|h,h' \in H,k,k' \in K\}
H × K = { ( h h ′ , k k ′ ) ∣ h , h ′ ∈ H , k , k ′ ∈ K }
容易验证直积是群。
定理 :如果m m m n n n
I m n ≅ I m × I n I_{mn}\cong I_m\times I_n
I m n ≅ I m × I n
定理 :如果G G G a , b a,b a , b m , n m,n m , n ( m , n ) = 1 (m,n)=1 ( m , n ) = 1 a b ab a b m n mn m n
定理 :
如果( m , n ) = 1 (m,n)=1 ( m , n ) = 1 ϕ ( m n ) = ϕ ( m ) ϕ ( n ) \phi(mn)=\phi(m)\phi(n) ϕ ( m n ) = ϕ ( m ) ϕ ( n )
如果p p p ϕ ( p e ) = p e − p e − 1 = p e ( 1 − 1 p ) \phi(p^e)=p^e-p^{e-1}=p^e(1-\frac{1}{p}) ϕ ( p e ) = p e − p e − 1 = p e ( 1 − p 1 )
如果n = p 1 e 1 ⋯ p t e t n=p_1^{e_1}\cdots p_t^{e_t} n = p 1 e 1 ⋯ p t e t ϕ ( n ) = n ( 1 − 1 p 1 ) ⋯ ( 1 − 1 p t ) \phi(n)=n(1-\frac{1}{p_1})\cdots(1-\frac{1}{p_t}) ϕ ( n ) = n ( 1 − p 1 1 ) ⋯ ( 1 − p t 1 )
剩余内容有些过于深入了,这里就只摘取可能与密码学有关的内容(有限群等)。
(柯西定理)如果G G G p p p G G G p p p
若p p p p 2 p^2 p 2