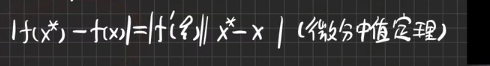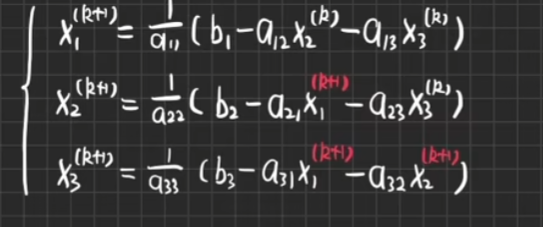《数值分析》复习笔记

一、绪论

数值计算算法设计的基本原则

1. 要有数值稳定性，能够控制舍入误差的传播；
2. 防止较小的数加到较大的数；
3. 避免两个相近的近似值相减；
4. 除法运算时，要避免除数的绝对值远远小于被除数的绝对值。

误差、有效数字

• 绝对误差：$e=x^*-x$，精确值减去近似值；
• 相对误差：$e_r = \frac{e}{x}=\frac{x^*-x}{x^*}$；
• 绝对误差限：$|e|\le \epsilon$。

有效数字：

上述（1）描述如何从绝对误差限推导有效数字，（2）描述从有效数字推导绝对误差。

绝对误差限一般为$0.5\times 10^n$，从第一个非零位到0.5之前那一位的数字个数就是有效位数。

绝对误差与函数：

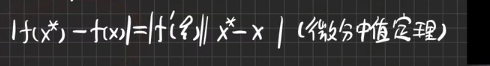
误差的计算方法

$$\epsilon(x\plusmn y ) = \epsilon(x)+\epsilon(y)\\ \epsilon(xy) = |x|\epsilon(y)+|y|\epsilon(x)\\ \epsilon(\frac{x}{y}) = \frac{|x|\epsilon(y)+|y|\epsilon(x)}{y^2}\\ \epsilon_r(a\plusmn b) = \frac{\epsilon(a)+\epsilon(b)}{|a\plusmn b|}\\ \epsilon_r(ab)\approx \epsilon_r(a)+\epsilon_r(b)\\ \epsilon_r(\frac{a}{b}) \approx \epsilon_r(a)+\epsilon_r(b)\\$$

衡量数值计算算法优劣的标准

1. 可靠的理论基础：正确性、收敛性、数值稳定性，是否可作误差分析；
2. 良好的计算复杂性：包括计算量和所占的内存空间。

二、线性方程组

范数

范数的性质：幺元、线性、三角不等式

常见的向量范数：

$$\displaystyle ||x||_1=\sum_{i=1}^n|x_i|\\ ||x||_2 = \sqrt{\sum_{i=1}^n x_i^2}\\ ||x||_\infty = \max_{1\le i\le n}|x_i|$$

相容范数：若对任意矩阵$A\in R^{n\times n}$，

$$||A|| = \max_{||x||=1}||Ax||$$

则由上式定义的$||\cdot||$是一种矩阵范数，其与所给定的向量范数相容，也称其为算子范数。

常见的矩阵范数：

$$\displaystyle 列范数||A||_1=\max_{1\le j\le n}\sum_{i=1}^n|a_{ij}|\\ 谱范数||A||_2 = \sqrt{\lambda_{max}(A^TA)}\\ 行范数||A||_\infty = \max_{1\le i\le n}\sum_{j=1}^n|a_{ij}|\\ F范数/欧几里得范数||A||_F = \sqrt{\sum a_{ij}^2}$$

矩阵的谱半径：

$$\rho(G) = \max_{i\le i\le n}|\lambda_i|$$

高斯消去法

能进行高斯消去的条件：前$n-1$个顺序主子式的行列式不为0。（第$i$个顺序主子式：左上角的$i\times i$元素构成的行列式）。

列主元高斯消去法

每次在消去前，将$a_{ik}^{(k)}$中绝对值最大的那一行换到第$k$行。

迭代法

$$Ax=b\\ \xRightarrow{A=N-P} Nx=Px+b\\ x= N^{-1}Px+N^{-1}b$$

收敛定理：对于迭代形式$x=Gx+d$，收敛的充分必要条件是$\rho(G)<1$，充分条件是$||G||\lt 1$。

$\rho(G)\lt ||G||$

迭代法的误差

$$||x^{(k)}-x^*||\le \frac{||G||^k}{1-||G||}||x^{(1)}-x^{0}||\\ ||x^{(k)}-x^*||\le \frac{||G||}{1-||G||}||x^{(k)}-x^{(k-1)}||$$

Jacobi迭代法

将矩阵$A$分解为$A=D+L+U$，则

$$x^{(k+1)} = -D^{-1}(L+U)x^{(k)}+D^{-1}b$$

收敛条件：

• 充要条件：$\rho(G)\lt 1$
• 充分条件$||G||\lt 1$
• 充分条件：矩阵$A$是主对角占优矩阵（主对角线绝对值比此列绝对值之和更大）。

Gauss-Seidel迭代法

令$A=D+L+U$，将$U$右移：

$$x^{(k+1)}=-(D+L)^{-1}Ux^{k}+(D+L)^{-1}b$$

实际上，为了避免计算$(D+L)^{-1}$，通常采用：

$$x^{(k+1)} = -D^{-1}Lx^{(k+1)}-D^{-1}Ux^{(k)}+D^{-1}b$$

收敛条件除了Jacobi方法相同的部分外，还加一条：系数$A$是正定的（特征值大于0）。

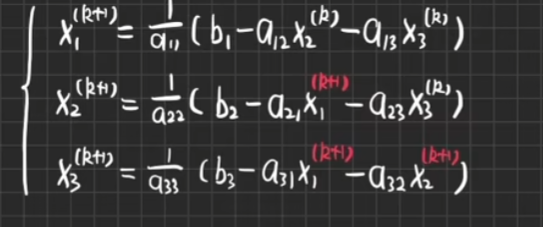
三、特征值

幂法求特征值

简单迭代：$u_k=A^ku$。

为了避免特征向量模过大，通常需要归一化：

$$\begin{cases} y_{k-1} = \frac{u_{k-1}}{||u_{k-1}||}\\ u_k = Ay_{k-1} \end{cases}$$

范数取二范数

$$\beta = y_{k-1}^Tu_k=y_{k-1}^TAy_{k-1}\\ \lim_{k\rarr\infty}\beta_k=\frac{\alpha_1x_1^T}{||\alpha_1x_1^T||}A\frac{\alpha_1x_1}{||\alpha_1x_1||}=\frac{\alpha_1^2x_1^Tx_1}{||\alpha_1x_1||_2^2}\lambda_1=\lambda_1$$

$$\begin{cases} \eta_{k-1}=\sqrt{u_{k-1}^Tu_{k-1}}\\ y_{k-1}=\frac{u_{k-1}}{\eta_{k-1}}\\ u_k = Ay_{k-1}\\ \beta_k = y_{k-1}^Tu_k \end{cases}$$

范数取无穷范数

$$\begin{cases} y_{k-1}=\frac{u_{k-1}}{||u_{k-1}||}\\ u_k = Ay_{k-1}\\ \beta = \frac{e_r^Tu_k}{e_r^Ty_{k-1}} \end{cases}$$

反幂法

$$Ax_i = \lambda_ix_i\\ A^{-1}x_i = \frac{1}{\lambda_i}x_i$$

原点偏移

$$Ax=\lambda x\\ (A-pI)x=(\lambda-p)x$$

则可求出$|\lambda_i-p|$最大的那个特征值。

幂法和反幂法的局限性

迭代是否收敛依赖于特征值的分布情况，不适合自动计算，只有矩阵阶数很高，无其他可用方法时，才用幂法和反幂法。

四、非线性方程求解

二分法

误差限$\epsilon=\frac{b_k-a_k}{2}$。

简单迭代法

收敛条件（需要两者都满足）：

• $\forall x\in[a,b], \phi(x)\in [a,b]$；
• $\forall x\in [a,b],|\phi'(x)|\le L\lt1$。

则：

• $x=\phi(x)$在$[a,b]$有唯一根s；
• $x_k\rarr s$;
• $|s-x_k|\le\frac{L^k}{1-L}|x_1-x_0|$
• $|s-x_k|\le\frac{L}{1-L}|x_k-x_{k-1}|$

可以压缩这个$[a,b]$区间，得到定理：$s=\phi(s)$，$\phi'(x)$在包含$s$的某个开区间内连续。如果$|\phi'(s)|\lt1$，则存在$\delta\gt0$，当$x_0\in[s-\delta,s+\delta]$时，由简单迭代法产生的序列 $x_k\rarr s$。

简单迭代法的收敛速度

若：

$$\lim_{k\rarr\infty}\frac{|e_{k+1}|}{|e_k|^k}=c$$

则称${x_k}$是$r $阶收敛的。

简单迭代法是$r$阶收敛的。

定理：若在$\phi^{(m)}(x)$在包含$s$的某个开区间内连续，如果

$$\phi^{(i)}(s)=0 \quad (i<m)\\ \phi^{(m)}(s) \ne 0$$

则简单迭代法以$m$阶速度收敛于$s$。

牛顿法

$$\phi(x) = x-\frac{f(x)}{f'(x)}$$

定理：$f(s)=0,f'(s)\ne 0,f''(x)\ne 0$，那么$\exist\delta$，使得

$$\begin{cases} x^0\in [s-\delta,s+\delta]\\ x^{k+1} = x^k-\frac{f(x)}{f'(x)} \end{cases}$$

二阶收敛到$s$。

下面这个定理给出一个更大的收敛区间：当下列条件满足时：

• $f(a)f(b)\lt 0$；
• $f''(x)$在区间$[a,b]$上不变号；
• $x\in[a,b],f'(x)\ne 0$；
• $x_0\in[a,b],f(x_0)f''(x_0)\gt 0$。

则由牛顿法产生的序列$x_k$单调收敛于根，并且是平方收敛的。

五、插值与逼近

插值多项式

拉格朗日多项式：

$\large\displaystyle f(x)=\sum_{i=1}^ny_il_i(x)$，其中$\large l_i(x)=\prod_{j=1,j\ne i}^n\frac{x-x_j}{x_i-x_j}$。

牛顿多项式：

.差商：$f[x_0,x_1]=\frac{f(x_1)-f(x_0)}{x_1-x_0}$，更一般地，$k$阶差商：$f[x_0,x_1,\cdots,x_k]=\frac{f[x_0,x_1,\cdots,x_{k-2},x_k]-f[x_0,x_1,\cdots,x_{k-2},x_{k-1}]}{x_k-x_{k-1}}$，打乱顺序不影响差商的值。

牛顿插值多项式为：

$$P_n(x) = f(x_0)+f[x_0,x_1](x-x_0)+f[x_0,x_1,x_2](x-x_0)(x-x_1)\\ + \cdots + f[x_0,x_1,\cdots,x_n](x-x_0)(x-x_1)\cdots(x-x_{n-1})$$

误差分析

牛顿插值公式（拉格朗日插值公式）的余项为：

$$R_n(x)=\frac{f^{(n+1)}(\zeta)}{(n+1)!}\omega_{n+1}(x)\\ \omega_{n+1}(x) = \prod_{i=0}^{n}(x-x_i)$$

差商与原函数的关系

$$f[x_0,x_1,\cdots,x_n] = \frac{f^{(n+1)}(\zeta)}{(n+1)!}$$

正交多项式系

函数的内积：

$$(f,g) = \int_a^b\rho(x)f(x)g(x)dx$$

若两个函数内积为零（如上式），则成$f,g$在$[a,b]$上带权$\rho(x)$正交。

正交多项式系的转化：将$\{\phi_0,\phi_1,\cdots,\phi_k\}$转化为正交多项式系：

$$\begin{aligned} \Phi_0(x) =& \phi_0(x)&\\ \Phi_1(x) =& \phi_1(x)& - \frac{(\phi_1,\Phi_0)}{(\Phi_0,\Phi_0)}\Phi_0(x)&\\ \Phi_2(x) =& \phi_2(x)& - \frac{(\phi_2,\Phi_0)}{(\Phi_0,\Phi_0)}\Phi_0(x)& - \frac{(\phi_2,\Phi_1)}{(\Phi_1,\Phi_1)}\Phi_1(x)\\ \Phi_i(x) =& \phi_i(x)&-\sum_{j=0}^{i-1}\frac{(\phi_i,\Phi_j)}{(\Phi_j,\Phi_j)}\Phi_j(x) \end{aligned}$$

最佳平方逼近

内积的的四个性质：可交换性、线性、可分可加性、非负性。

最佳平方逼近希望解决的问题是，使用简单函数$p(x)$去逼近$f(x)$，其中$p(x)$是从子空间$H_n=Span\{\phi_1,\phi_2,\cdots,\phi_n\}$中的函数线性组合成的，找到的这个$p^*(x)s$是最佳平方逼近元素。

定理：$p^*(x)$是最佳平方逼近元素时的充分必要条件是：$(f-p^*,\phi_i)=0$。

这个定理可以从三维向量空间的几何直观去理解。

六、数值积分

代数精度

$$\int_a^bf(x)dx \approx \sum_{k=0}^n\lambda_kf(x_k)$$

当$f(x)$为任何次数不高于$m$的多项式时等式成立，而当$f(x)$为某个$m+1$次多项式时等式不成立，则乘该求积公式有$m$次代数精度。

插值型积分公式

$$\int_a^bf(x)dx\approx \sum_{k=0}^n\lambda_k^{(n)}f(x)\\ \lambda_k^{(n)} = \int_a^bl_k(x)dx$$

其截断误差为：

$$R_n = \int_a^b \frac{f^{(n+1)}(\xi)}{(n+1)!}\prod_{j=0}^n(x-x_j)dx$$

定理：$n+1$个节点的插值型求积公式至少有$n$次代数精度。

定理：如果$n+1$个节点的求积公式有大于等于$n$次的代数精度，则该公式为插值型求积公式。

梯形积分

$$\int_a^bf(x)dx\approx \frac{b-a}{2}[f(a)+f(b)]$$

其截断误差为：

$$R_1 = -\frac{(b-a)^3}{12}f''(\eta), \ \eta \in (a,b)$$

梯形公式具有一次代数精度。

Simpson积分

$$\int_a^bf(x)dx \approx \frac{b-a}{6}\left[ f(a)+ 4f(\frac{a+b}{2})+f(b)\right]$$

其截断误差为：

$$R_2 = -\frac{(b-a)^5}{2880}f^{(4)}(\eta)$$

Simpson积分有3次代数精度。

高斯型积分公式

高斯型积分公式是试图手动确定节点的位置，来实现更高的代数精度。

定理：求积公式是高斯型求积公式的充分必要条件是它的求积节点是$n$次正交多项式$g_n(x)$的$n$个零点。（注意带权函数）

求积系数为 $A_i=\int_a^b\rho(x)l_i(x)dx$。

截断误差为：

$$R = \frac{f^{(2n)}(\eta)}{a_n^2(2n)!}\int_a^b\rho(x)g_n^2(x)dx$$

故其代数精度为$2n-1$。

七、常微分方程初值问题解法

初值问题

$$\begin{cases} y' = f(t,y)\\ y(t_0) = y_0 \end{cases}$$

求上述$y(x)$表达式的问题即为初值问题。

李普希兹条件：$\forall u_1,u_2, |f(t,u_1)-f(t,u_2)|\le L|u_1-u_2|$。

若李普希兹条件成立，则该初值问题有解且唯一。

显式单步法（欧拉法）

显式单步法的一般形式是：

$$y_0 = y(x_0)\\ y_{n+1} = y_n + hf(t_n,y_n)$$

隐式欧拉法

$$y_0 = y(x_0)\\ y_{n+1} = y_n + hf(t_{n+1},y_{n+1})$$

两步欧拉

$$y_{n+1} = y_{n-1} + 2hf(x_n,y_n)$$

梯形公式

$$y_{n+1} = y_n + \frac{h}{2}[f(x_n,y_n)+f(x_{n+1},y_{n+1})]$$

梯形公式法可以看成显式、隐式欧拉法的平均，该方法本质还是隐式的。

改进欧拉法

先用显式欧拉法对$y_{n+1}$进行预测，算出$\bar{y}_{n+1}=y_n+hf(x_n,y_n)$。

再将这个预测值带入隐式的梯形公式：

$$y_{n+1} = y_n + \frac{h}{2}[f(x_n,y_n)+f(x_{n+1},\bar{y}_{n+1})]$$

另一种表达为：

$$y_p = y_n + hf(x_n,y_n)\\ y_c = y_n + hf(x_{n+1},y_p)\\ y_{n+1} = \frac{1}{2}(y_p+y_c)$$

该方法也称为预估-校正法。

截断误差

初值问题单步法的一般形式为：

$$y_{n+1} = y_n + h\phi(x_n,y_n,y_{n+1},h)$$

整体截断误差为：$\epsilon_n= y(x_n)-y_n$，实际上$y_n=y_{n-1}+h\phi(x_n,y_{n-1},y_{n},h)$中，$y_{n-1},y_{n}$是会逐步影响后序解的，所以一般使用局部截断误差$R = y(x_n)- [y(x_{n-1})+h\phi(x_{n-1},y(x_{n-1}),y(x_n),h)]$，将$y_n$暂时认为是精确值。

局部截断误差比较

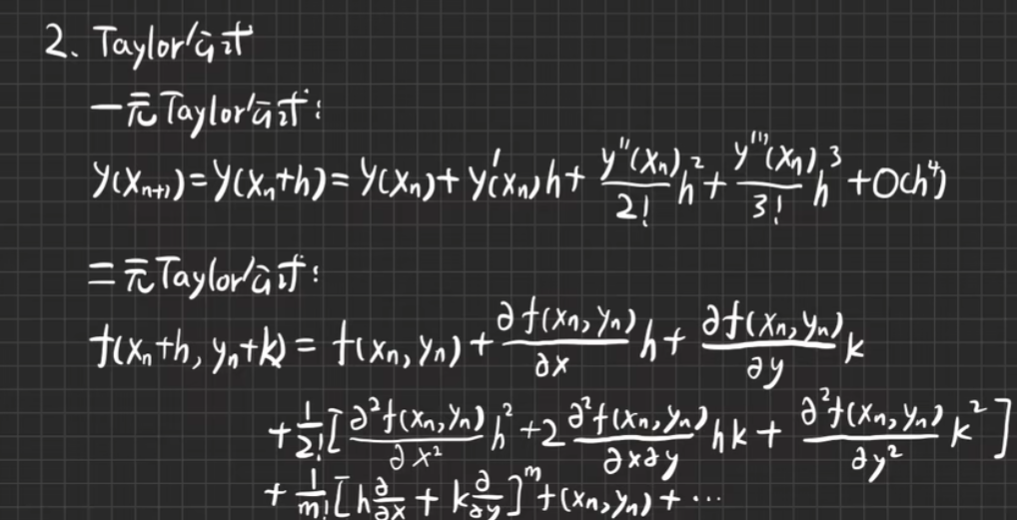
• 显式欧拉法：$R=\frac{h^2}{2}y''(x_n)+o(h^3)$（一阶方法）
• 隐式欧拉法：$R=-\frac{h^2}{2}y''(x_n)+o(h^3)$（一阶方法）
• 梯形公式法：$R= -\frac{h^3}{2}y'''(x_n)+o(h^4)$（二阶方法）

计算截断误差阶数的方法：将$R = y(x_n)- [y(x_{n-1})+h\phi(x_{n-1},y(x_{n-1}),y(x_n),h)]$的方括号里的项运用二元泰勒公式，再对$y(x_n)$运用一元泰勒公式，比较其对应的项。

精度

若单步差分公式的局部 截断误差为$o(h^{p+1})$，则该公式为 $p$阶方法。

方法的分析

相容性

相容性是指：

$$\lim_{h\rarr0}\phi(t,y(t),h)=f(t,y(t))$$

成立。

如果增量函数$\phi(t,y,h)$连续，且对变量$h$满足李普希兹条件，则单步法与微分方程相容的充分必要条件是单步法至少是一阶的方法。

收敛性

如果下式成立

$$\lim_{h\to0} y_n=y(t)$$

则称单步法为收敛的。或通过整体截断误差：

$$\lim_{h\to0}\epsilon_n=0$$

上述两式是等价的。

定理：如果增量函数$\phi(t,y,h)$连续，并对变量$y$和$h$满足李普希兹条件，且单步法与微分方程形容，则单步法是收敛的。

绝对稳定性

绝对稳定性是指当初值有误差$e_0$时，后续的误差将收敛到0：

$$\lim_{n\to\infty}e_n = 0$$

考虑绝对稳定性时，一般只考虑如下的线性常系数微分方程：

$$y'=\lambda y$$

在计算绝对稳定性时，首先得到迭代格式。尝试展开迭代格式，然后将$y'=f(t,y)$代入，再将$y'=\lambda y$代入，则可以得到$y_{n+1}=\Phi(h,\lambda)y_n$，求解$|\Phi(h,\lambda)|\lt1$这个不等式即可。

以二级二阶R-K公式为例，其迭代格式如下：

$$\begin{cases} y_{n+1}=y_n+\frac{h}{2}(k_1+k_2) \\ k_1 = f(t_n,y_n)\\ k_2 = f(t_n+h,y_n+hk_1) \end{cases}$$

可以先将$k_1,k_2$用$y_n$表达出来：

$$k_1 = f(t_n,y_n)=y'(t_n)=\lambda y(t_n)=\lambda y_n\\ k_2 = f(t_n+h,y_n+hk_1) = y'(t_{n+1}) = \lambda y(t_{n+1})=\lambda(y_n+hk_1) = \lambda(y_n+h\lambda y_n)$$

将$k_1,k_2$代入$y_{n+1}$的表达式：

$$y_{n+1} = y_n+\frac{h}{2}(\lambda y_n+\lambda (y_n+h\lambda y_n))\\ = (1+h\lambda+\frac{(h\lambda)^2}{2})y_n$$

同理，欧拉法求初值问题的公式为：

$$y_{n+1} = (1+h\lambda)y_n$$